Entropy and Outlier Calibration in Language Mixture Models
The patent “Detecting extraneous topic information using artificial intelligence models” hints at the importance of applied information theory in calibrating industrial mixture models. We use this as motivation to understand information theoretic tools, focusing on entropy and perplexity.
Disclaimer: I’m a co-inventor on this patent, though the legal rights are held by my former employer, Invoca, Inc. The views expressed in this post are my own and do not necessarily reflect the views of my former employer or the current assignee of the patent mentioned. The mathematical examples and interpretations provided here are for educational purposes and are intended to illustrate general principles of information theory.
Mixture Models
Mixture Models assume the data is generated by a combination of several distinct distributions. The challenge is that some of those ‘components’ in the mixture represent meaningful signal, while others inevitably absorb the background noise. When training a model to understand language, the system often gets distracted by filler words, document artifacts, and other sources of noise.
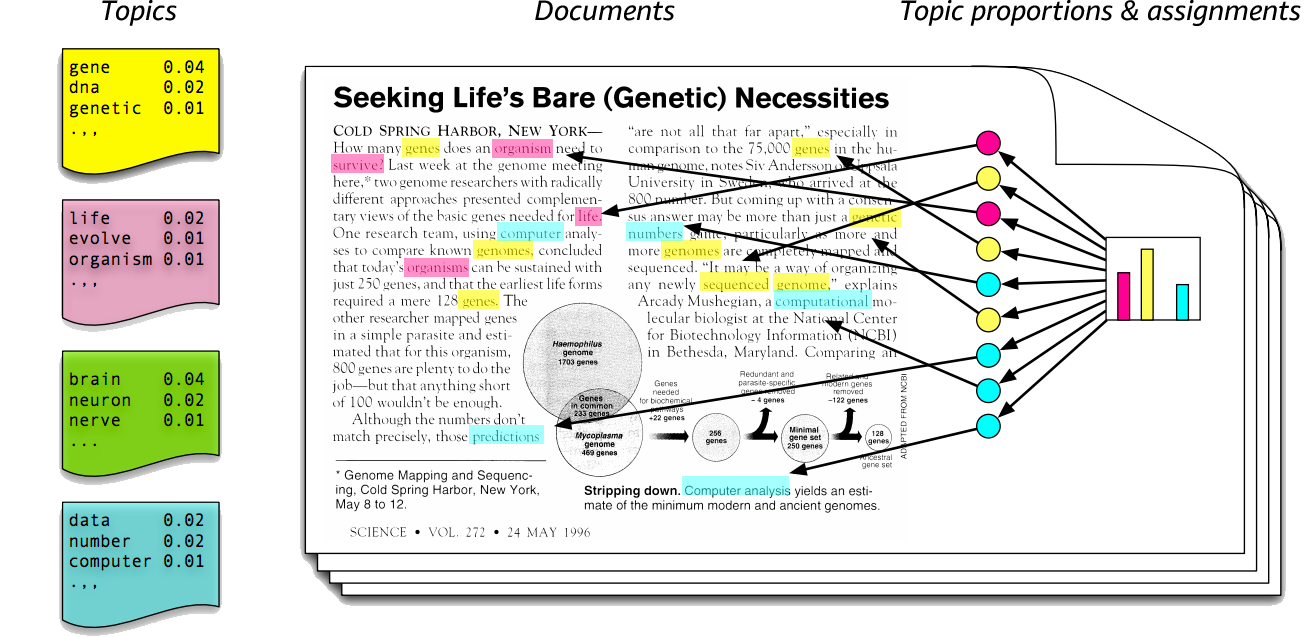
Consider Latent Dirichlet Allocation on documents (credit) in the diagram. Each document is decomposed into words, which are generated from topics, where the set of topics is learned from a larger corpus. Each document is then a mixture of topics. The model is forced to explain everything in the text, even if it isn’t interesting to humans.
Consider two extreme examples of rogue probability distributions:
- Uniforms, so generic that the model is not useful
- Concentrated spikes, so specific that it’s likely overfitting to structured noise
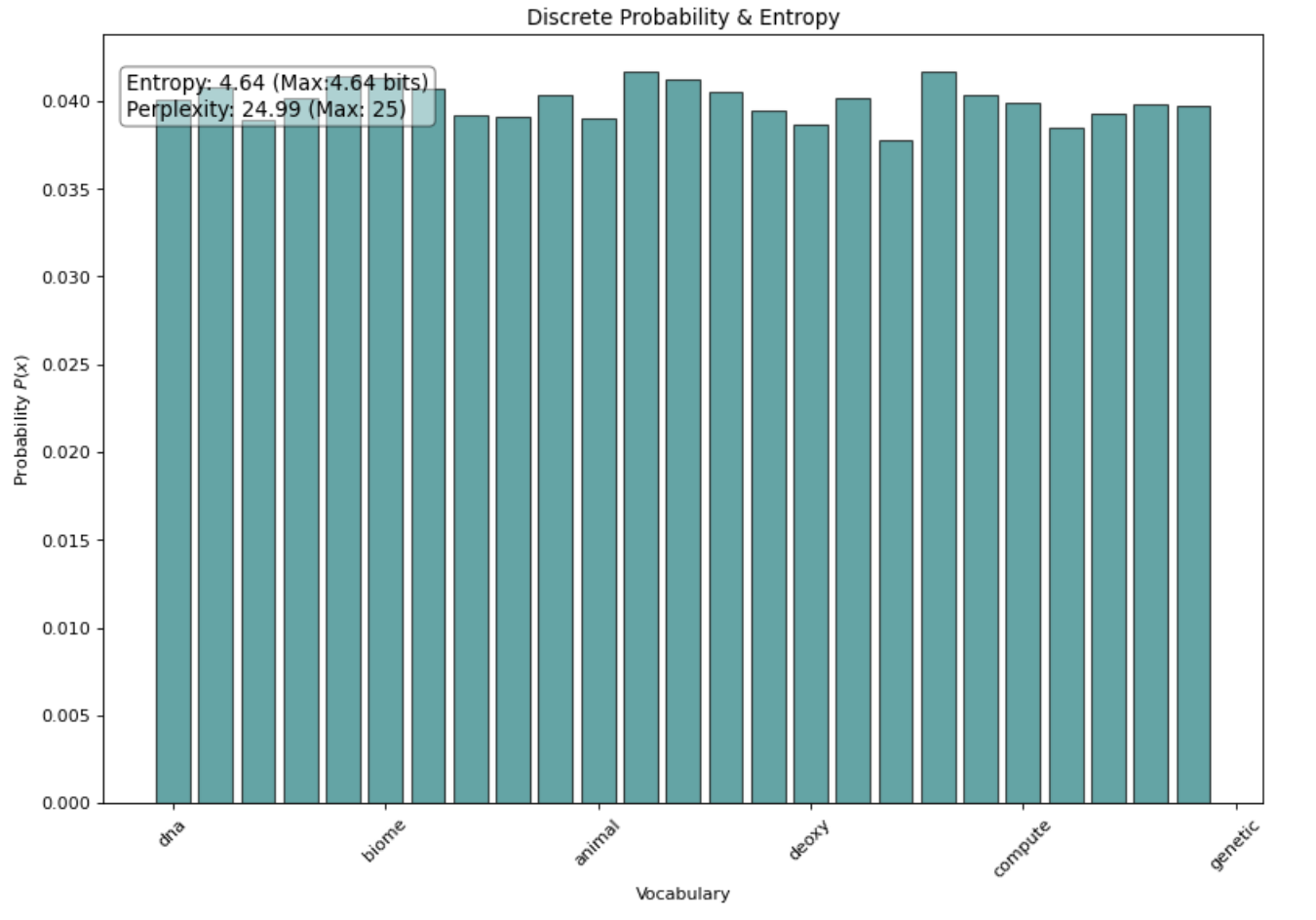
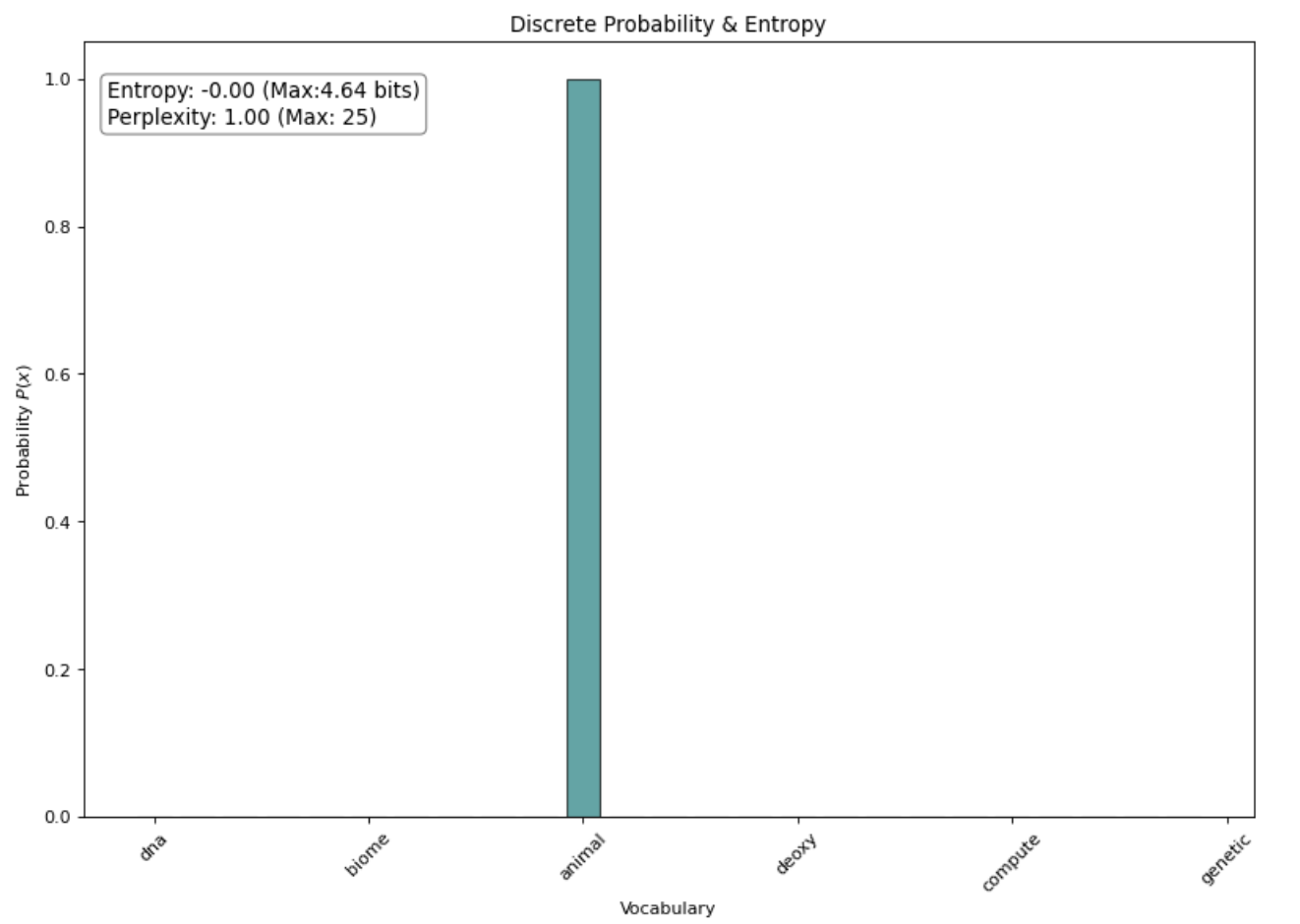
These are outlier distributions in entropy space, even though models often produce them in practice! So, what can we do?
The Patent: Entropy-Based Topic Calibration in Practice
One key result* of the patent is that for topic models (a class of mixture model), entropy can be used to calibrate “topics”, which are mixtures of word-level probability distributions. Specifically, they emphasize the relationship between entropy and “effective vocabulary size”, which is a common interpretation of perplexity on language datasets.
Main takeway: information theory gives us entropy and perplexity to describe concentration in probability distributions. In many settings, including in this patent, these calculations provide a powerful foundation for filtering noise.
* The patent has a lot more to say. The product, data, specific model, and other details in the patent are out of scope for this educational post, though worth a read!
Entropy
Formally, entropy is the expectation of the negative log probability of a distribution. It is an information-theoretic value, important in many fields like computer science and physics. The calculation is straightforward,
\[H(X) = - \sum_x P(x) \log_2(P(x))\]where the sum over \(x\) is just a weighted average over the items in the distribution.
A practical view of entropy is as “concentration” in probability mass, or uncertainty. The entropy Wikipedia article nicely demonstrates this with the above plot of entropy as a function of a weighted coin’s probability.
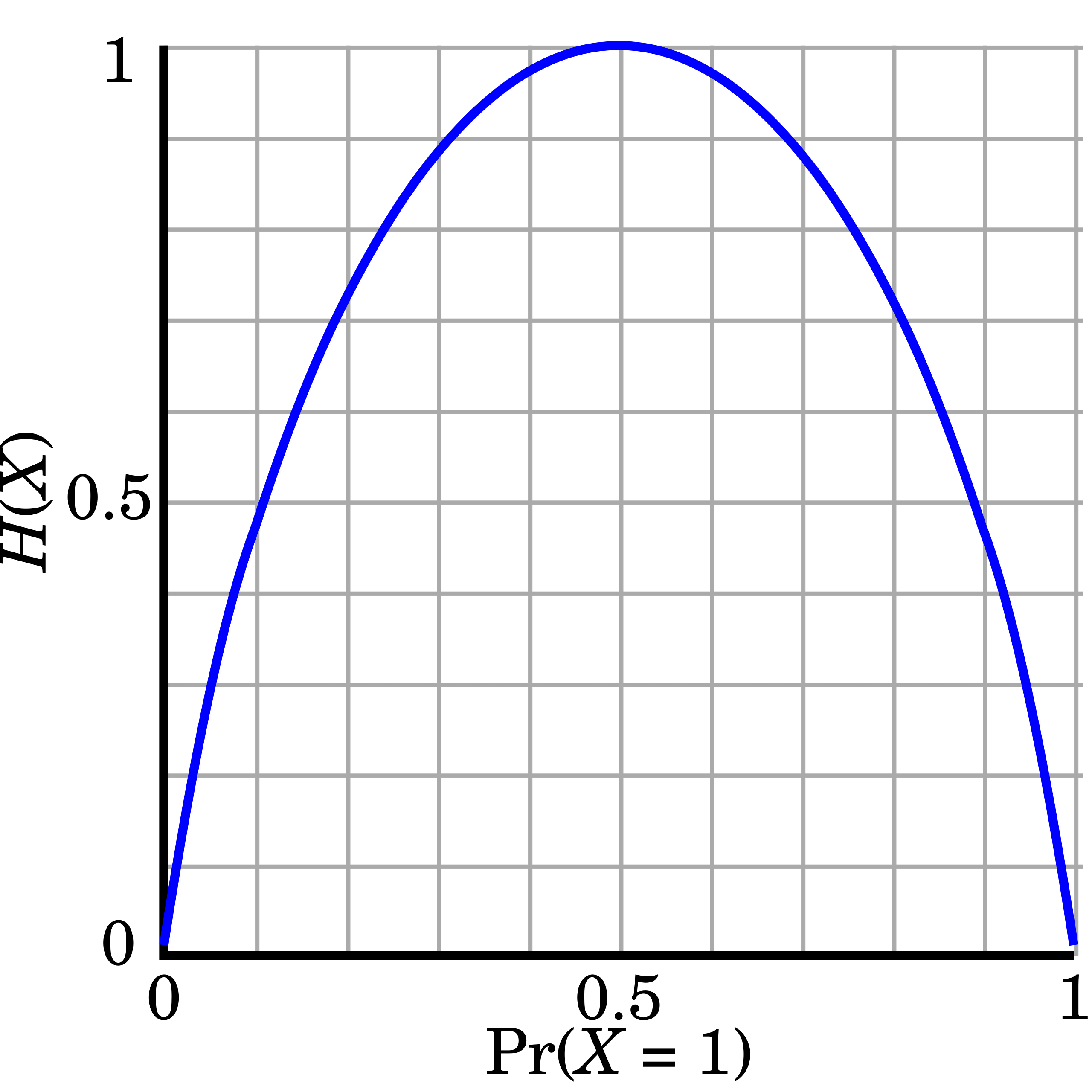
Low entropy is associated with high concentration, or low uncertainty. High entropy means maximum uncertainty – the outcome can be any of the states since the probability weight is diffuse.
In short, the plot shows the following:
- Entropy is minimized when
P(X) = 1orP(X)=0since the outcome is absolute - Entropy is maximized when
P(X) = 0.5because the coin’s uncertainty is maximized
For another point of view, consider a 25-sided dice roll. If we start with all probability mass on 1 state, then gradually spread the probability among other states, we can see that the entropy trends toward its maximum value at a uniform distribution.
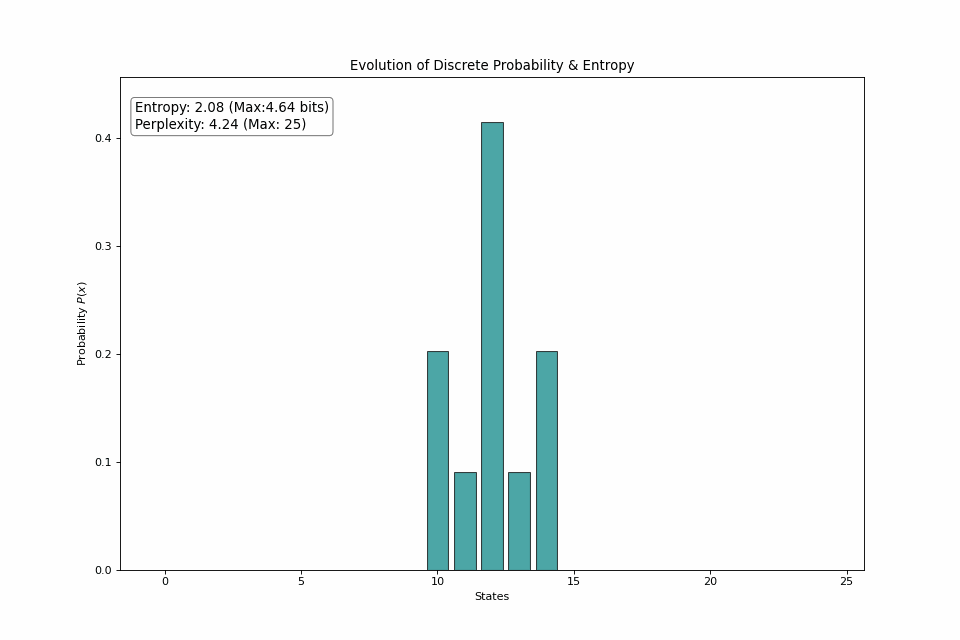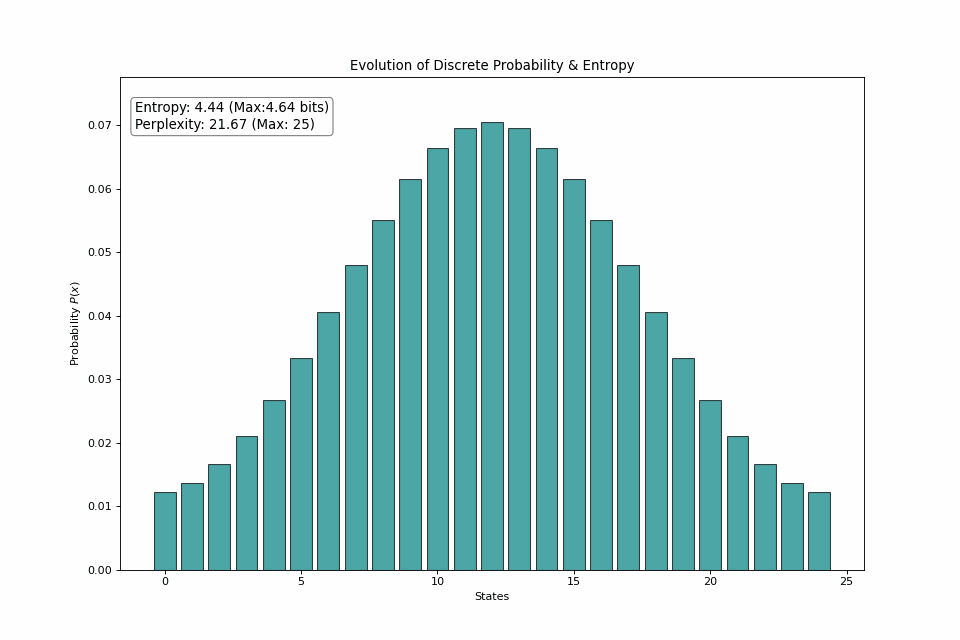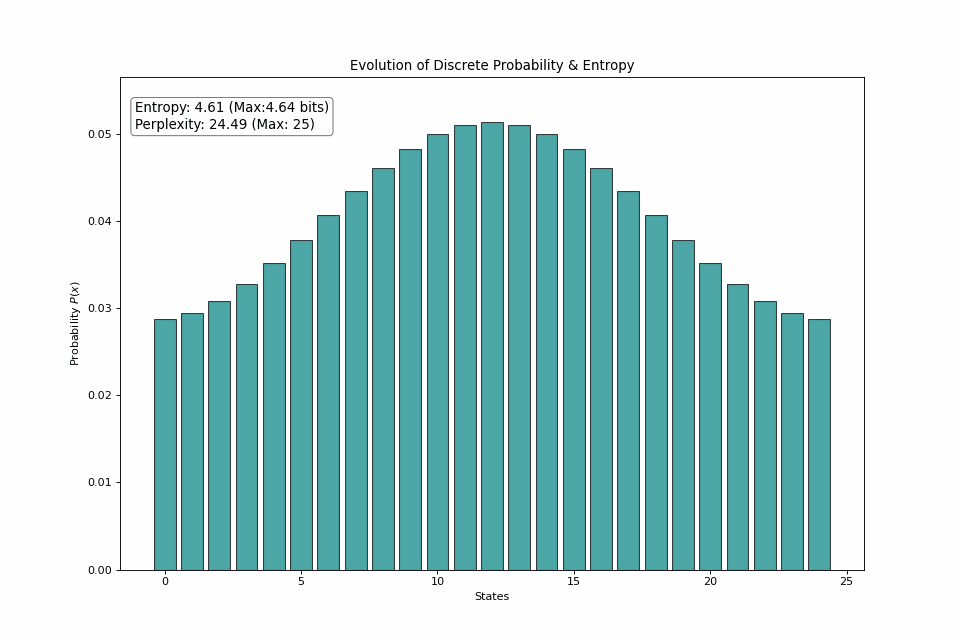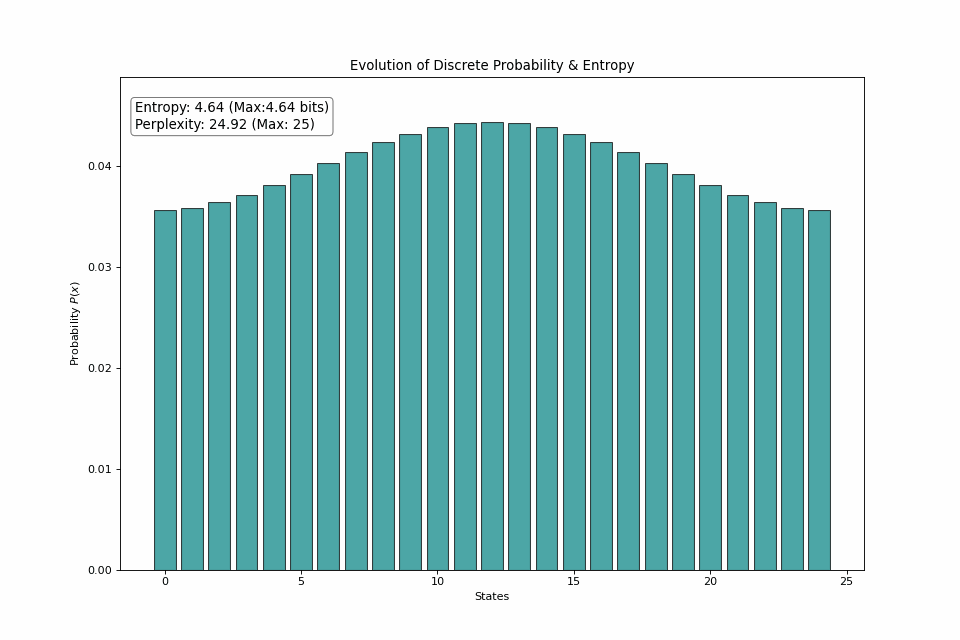
The dice roll shifts from returning the same side every roll to picking from a side at random, bringing the number of realistic outcomes from 1 to the full 25.
Perplexity: The Effective Number of States
Perplexity converts the abstract entropy (in bits) to something human interpretable. The value, which we will call \(PP\) for short, is the effective number of states. When the distribution is over words (e.g. language modeling or topic models), perplexity is often interpreted as an effective vocabulary size.
If entropy is \(H(x)\), perplexity is a simple calculation:
\[PP(X) = 2^{H(X)}\]or, its full form:
\[PP(X)= 2^{ -\sum P(x)\text{log}_2(P(x))}\]For example, consider if our 25-sided die is heavily weighted toward only two numbers, its entropy might be ~1 bit. Taking \(2^1\) gives us 2 effective states. This tells us that despite the 25 possible outcomes, the model is effectively ‘seeing’ only two.
Perplexity is powerful because it quantifies concentration of a probability distribution in a human-friendly way!
Putting the Math to Use: Analyzing Distributions
Entropy and perplexity describe probability distributions. With them, we can quantify intuitive notions like “concentration”, “sharpness”, or “broadness”. Further, with these descriptions in mind, a domain expert can provide guardrails on their mixtures that factor in the type of distribution that is actually desirable!
The ultimate goal of identifying and handling outliers falls on the domain expert to implement – every problem is different. However, this framework is broadly applicable!
Consider a basic case study: For a distribution over 10,000 unique words in a topic modeling problem, we can inspect some typical cases and edge cases with made up numbers:
| Scenario | Entropy (\(H\)) | Perplexity (\(2^H\)) | Interpretation | Calibration Action |
|---|---|---|---|---|
| Absolute Certainty | 0 bits | 1 word | The distribution is a single spike on one word. | Filter: Overfit |
| Overly-Focused | 3 bits | 8 words | Concentrated on a small vocabulary. | Filter: Overfit to structured noise |
| Organic Category | 6-8 bits | 64 - 256 words | Sweet spot: not too many or too few words. | Keep: High likelihood of real signal |
| Generic | 10 bits | 1,024 words | Diffuse noise; the model is “guessing.” | Filter: Extraneous |
| Uniform Noise | \(\log_2(10,000) \approx 13.3\) bits | 10,000 words | Maximum uncertainty; no pattern learned. | Filter: Total Noise |
Conclusion
Mixture models are powerful precisely because they try to explain everything—but that strength is also a liability. In practice, some components inevitably drift toward extremes: overly sharp distributions that memorize structured noise, or overly diffuse distributions that capture nothing meaningful at all. These failure modes are not bugs; they are natural consequences of fitting probabilistic models to messy, real-world data.
Entropy and perplexity give us a principled way to reason about these behaviors. Rather than inspecting topics qualitatively or relying on ad hoc heuristics, we can quantify how concentrated or how diffuse a distribution really is, and compare it against what makes sense for a given domain. Interpreted correctly, perplexity becomes an intuitive proxy for “effective complexity,” such as the number of words a topic meaningfully uses.
The key takeaway is not that entropy provides a universal threshold or automatic solution. Instead, it provides a calibration signal—one that allows domain experts to set informed guardrails around their mixture components, filter extraneous noise, and focus modeling capacity where it matters most. While this post focused on topic models, the same ideas extend naturally to other probabilistic mixtures and modern language systems.
Disclaimer: The views expressed in this post are my own and do not necessarily reflect the views of my former employer or the current assignee of the patent. The mathematical examples and interpretations provided here are for educational purposes and are intended to illustrate general principles of information theory.